“Mathematics is the language in which God has written the universe.” – Galileo

My daughter is in 5th grade and this is our second year approaching math in a way I believe stands apart from most K-12 schools. It has led to some interesting developments, including declarations of, “Math is my favorite subject!” and “Can you pleeeeease tell us another math puzzle?” Let me tell you a bit about how we got here.

We left public school four years ago. (My goodness!) That’s when I first encountered the debates in math instruction (e.g. direct instruction vs. discovery, spiral vs. mastery.) I narrowed our curricular choices and went with one textbook that did a great job of explaining place value. It came with manipulative blocks and instructional videos; it was a great blend of support and hands-on learning for our 2nd grader (at the time) and for me as a new homeschooler.

Ten chicks have I. Four of them are yellow, Four of them are brown, Four of them are speckled. The nicest in the town.

Fairly quickly into our homeschooling journey I started reading about education philosophy and discovered the works of the early 1900s British educator Charlotte Mason. I started implementing as I learned the methods and optimized as I deepened my study. Mason’s method calls for a wide feast of subjects to be presented to children. These include Bible, poetry, literature, history, art, music, nature study, math, science, ancient and modern languages. Short lessons and student narration are brilliant tools. All together, these do form a beautiful feast of ideas.

To use modern education parlance, this is a knowledge-rich curriculum. Mason’s principles are over a hundred years old and will take you far but there are still areas for you as the educator to fill in, e.g. choosing your own phonics programs, supports for students with special needs, math curriculum, etc.

I kept reading and implementing. Over time, I came to three major math realizations:

1. A Mason-inspired math approach works very well for teaching new concepts. First, I introduce a new concept with concrete examples (manipulatives or household items) to show how a concept works. Example: Let’s slice some apples into quarters and then eighths and add the pieces using fractions—then we’ll eat them. Next lesson, move up one level of abstraction. Example: let’s draw some apple slices on the board and learn to write the fraction. The next lesson will move up another level of abstraction. Example: A problem set that includes questions like 3/4 + 3/4 = ?

2. Number sense isn’t glamorous but math facts are building blocks of math. Putting in the practice/memory work here will lead to more automaticity and fluency in math. It’s going to be harder for a kid to multiply fractions if much of their mental load is taken up by trying to figure out basic multiplication. This doesn’t mean drilling mindless memorization. Games make learning math facts fun.

3. Math is beautiful and it must be taught as such. I can’t imagine Mason would have accepted math educators who approached math with disdain, which includes treating math like a chore. It seems at the very least, math should have a proper place in the “feast” of ideas we set before children. I was using a solid math curriculum but I had been treating math like a one-a-day vitamin; it was necessary, but not savored. I was not sharing the beauty of math as well as I could. When I changed this, everything changed.

Suddenly, math was a far more delectable part of the education feast.

I started to keep an eye out for interesting math books whenever I was in a used book stores. I started collecting recommendations from mathy moms. Right around this time Julia started playing chess. She also started asking me for more “thought puzzles” which I base on old law cases. She’s 10 now and we seem to have hit our stride when it comes to mathy subjects and critical thinking. Now that I think of it, it may not be a coincidence that this happened the same year she’s been working on an Ancient Greek language code cracking book; I believe the part of the brain that learns a new code/language overlaps with the part that does math.

A week of math now looks like:

• Doing math from our MUS “Epsilon” book, 3-4 days a week. Note: this is an old photo with last year’s Delta book from the same publisher.
• Logic games (more on this below)
• A selection from our Algebra and Geometry books 2-3 days a week.
• Playing math. E.g. Kicking a soccer ball back and forth and practicing mental math.
• Reading interesting, well-written books about math as read-alouds.
• Working on chess problems together (great for reasoning and doubles as chess practice.) “Spectacular Chess Problems” is excellent.
• Discussing a math puzzle or “older” math concept. These can take a couple days to work out! A princess is trapped on an island surrounded by a square moat that measures 20′ across. A knight has two 19′ beams. This one led to so many questions before she found the answer!
• Math games — just for fun, not assigned

From Heart of Mathematics. 

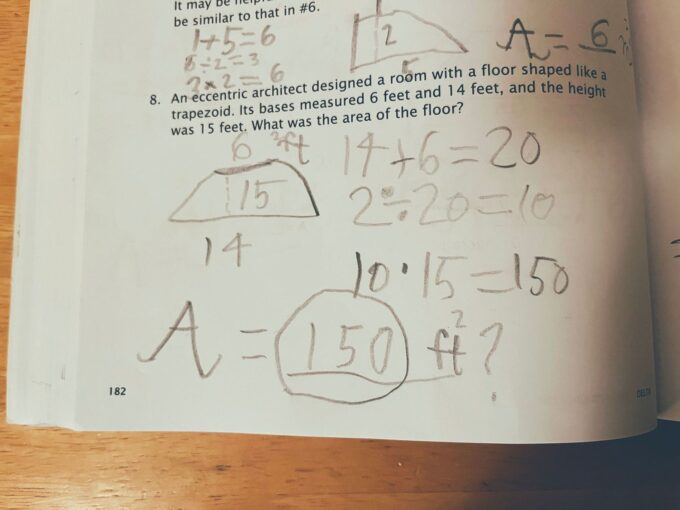From Delta workbook

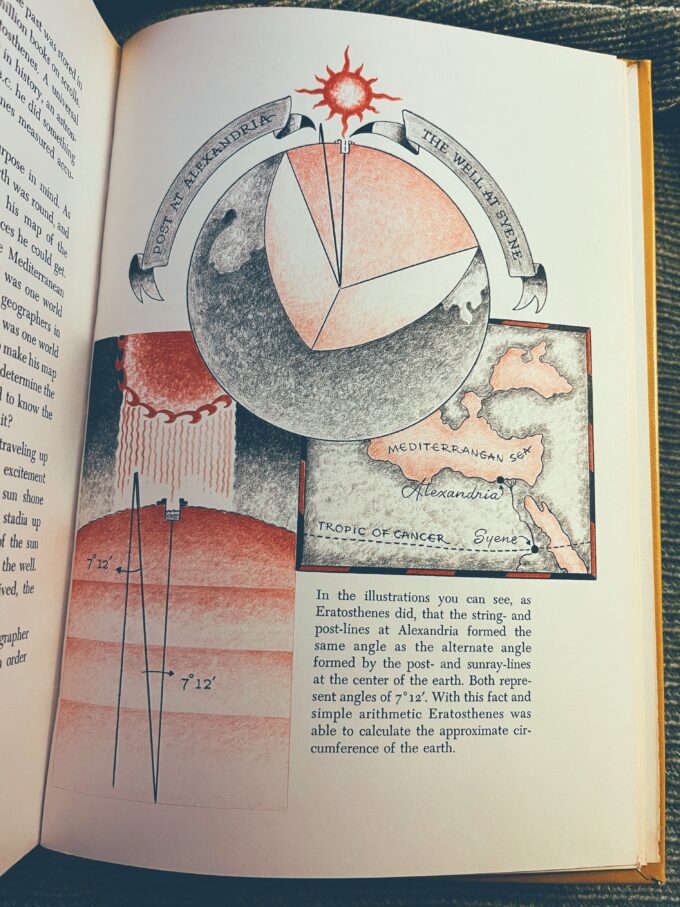From Story of Geometry

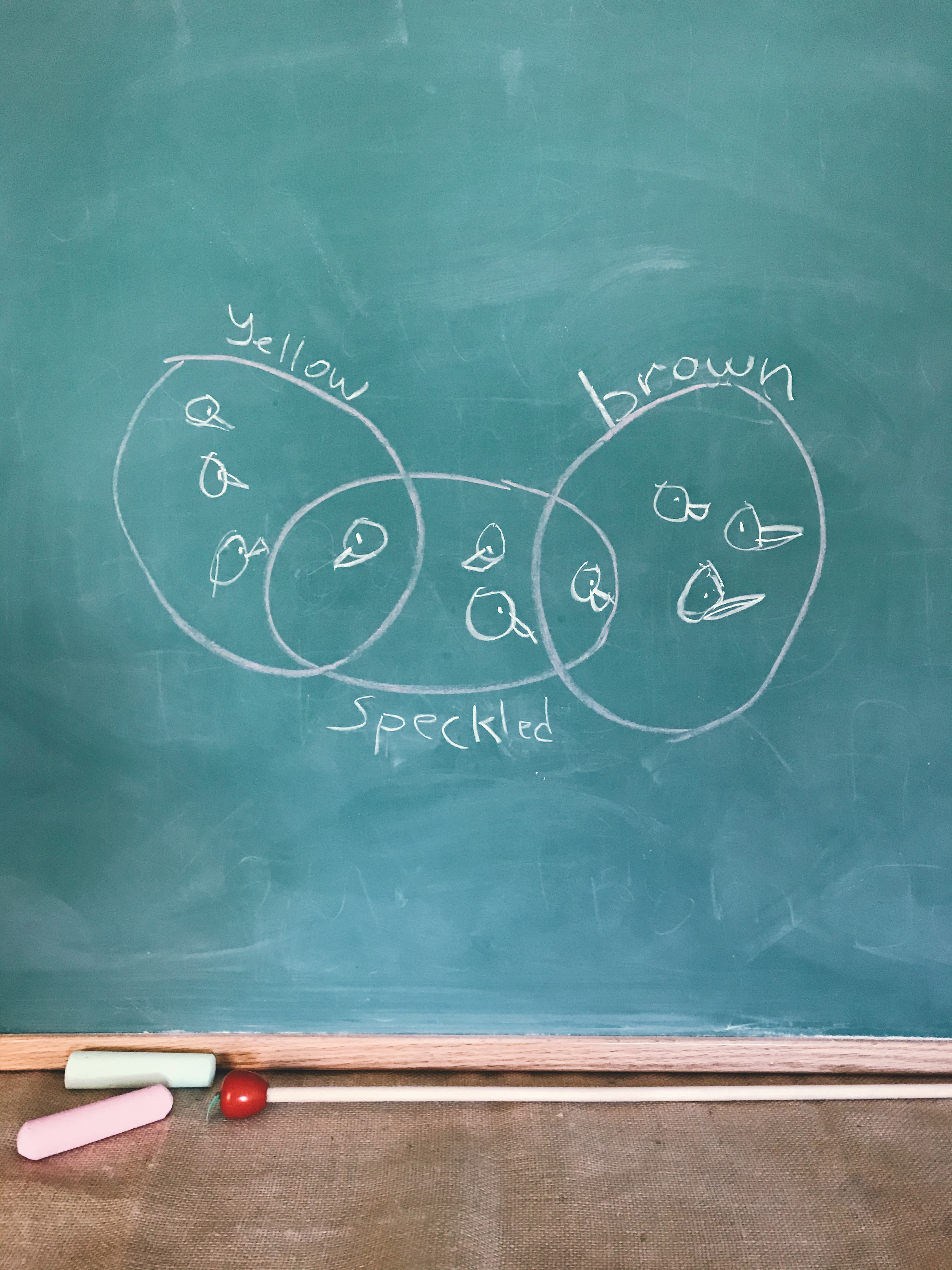
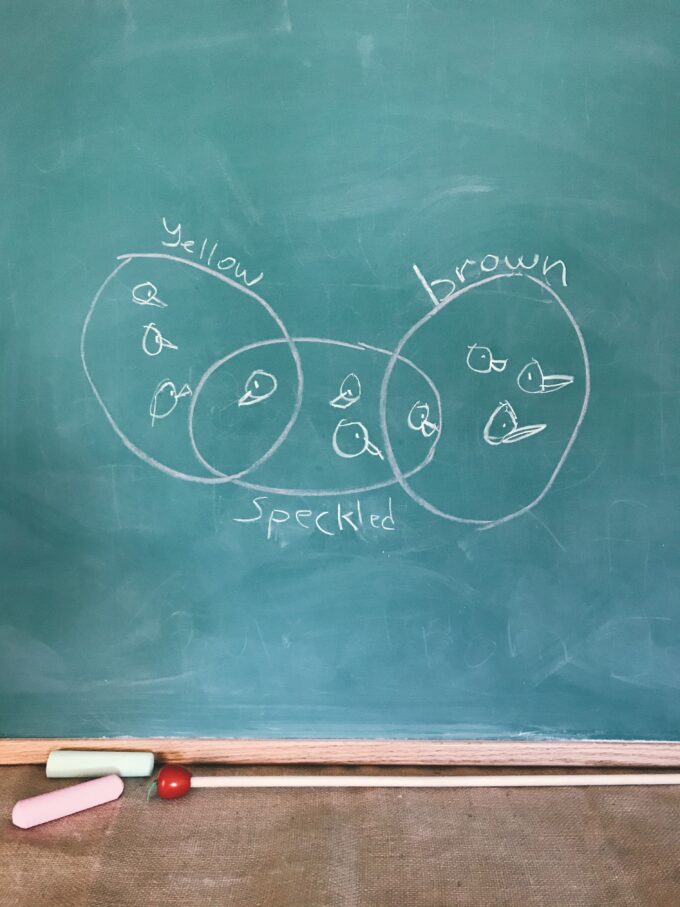
The above is from our Geometry textbook which has a nice long introduction on logic and reasoning. She recently learned about Euler diagrams with this book.

Allow me to get a bit romantic for a second. I have fond memories of taking formal logic at UC Berkeley, where I graduated with a degree in Philosophy. If you’re familiar with the campus, the classes were in the Hearst Memorial Mining Building. The lecture hall there is airy and oak-lined and our professor was wonderful. I just can’t help but be nostalgic as I draw familiar shapes on the board for my daughter. I met my husband at Berkeley, so there’s no Julia without Berkeley. I’m grateful for all the echoes in our lives of that special place and there lessons learned there.

Anyway! Euler diagrams can look like this. My first example to her was A->B; “If I’m riding the teacups, then I’m at Disneyland.”

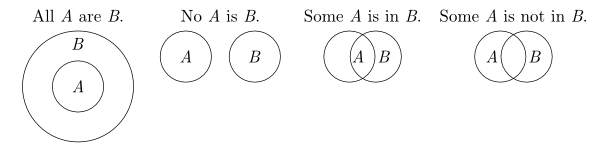
She understood the validity and invalidity of the converse, contrapositive, and inverse, even though she doesn’t know those terms yet.

Why a child can understand logic or math concepts that seem “beyond them” is beyond me. But I believe reason is one of the many gifts from God. An introduction to logic has enabled her to work on logic puzzles that I give her. I was a bit hesitant about this because Charlotte Mason cautioned against too great a focus on analytic thinking in early education, favoring “synthetic,” connection-making, thinking instead. However, I feel we live in an age of unreason; we must equip our kids with the ability to think with clarity, discernment, and elegance.

I spent this whole post discussing math with my 10-year-old, but we “play math” with my 4-year-old too. No workbooks, just play, hands-on stuff, and beautiful books which occasionally include numbers. She enjoys NumberBlocks on Netflix (awesome show!) She loves counting and picked this as her favorite book last summer:

As I traverse this piece of the universe with my kids, I will try my best to marvel at the beauty of numbers and logic alongside them. Here are some quotes that got me thinking more about math education.

Quotes that got me thinking more about math education…

“Pure mathematics is, in its way, the poetry of logical ideas.” – Albert Einstein

“Children have a birthright to knowledge about God, man, and the universe.”- In Vital Harmony by K. Glass, a book about Charlotte Mason’s education philosophy

“Math is objectively true, good, and beautiful. Math doesn’t change, but I can. So I can come to appreciate math and conform my perception to reality more and more.” – Schole Sisters podcast #98 Ordo Amoris

“Mathematics is the language in which God has written the universe.” – Galileo

“Euclid alone has looked on Beauty bare.” – Edna St. Vincent Millay

“I am quite convinced; and, believe me, if I were again beginning my studies, I should follow the advice of Plato and start with mathematics.” – Galileo

“The child may learn the multiplication-table and do a subtraction sum without any insight into the rationale of either. He may even become a good arithmetician, applying rules aptly, without seeing the reason of them; but arithmetic becomes an elementary mathematical training only in so far as the reason why of every process is clear to the child.” – from Home Education, Vol. 1, Section 15 Arithmetic by Charlotte Mason

“The principality of mathematics is a mountainous land, but the air is very fine and health-giving, though some people find it too rare for their breathing. People who seek their work or play in this principality find themselves braced by effort and satisfied with truth.” – Charlotte Mason

One quote from Joan Didion’s “Blue Nights,” from a passage recounting her daughter’s illness and passing, has stayed with me ever since:

“We wished them happiness, we wished them health, we wished them love and luck and beautiful children. On that wedding day, July 26, 2003, we could see no reason to think that such ordinary blessings would not come their way. Do notice: We still counted happiness and health and love and luck and beautiful children as “ordinary blessings.”

Motherhood can feel like one long procession of the ordinary: waking night after night to help a little child, lulling, assuaging, making spaghetti, helping wash their hands, combing hair, reading book after book, standing by playground structures, reminding kids to use good manners, answering endless questions, driving them places, brushing teeth, sitting together in awed contemplation of life’s mysteries, and folding laundry.

Then I became a homeschooling mom: reading several books at once, teaching long division, reading book lists at 2 am next to my sleeping husband, listening to podcasts about education, supervising science experiments, teaching my littlest letters and numbers, gathering art supplies, cleaning up after art has been made, driving to extracurriculars and park days and field trips, poems over breakfast, discussions over lunch, leaving the library with giant bags full of books.

Didion reminds me that my ordinary blessings are tremendous gifts. As the end of another homeschool year approaches, I am so grateful. A mama with a few decades of homeschooling experience told me that I might expect one or two perfect days in a homeschool year. Some good days. Many ordinary days. Some bad days. God blessed me with many good days and many ordinary days. What more can I ask?

If you ever wanted to talk, in real life, about homeschool, we could talk for hours. I love all the meaty stuff: every homeschool curricula on the market, the different pedagogical approaches, the challenges and wins, all of it. This is not that. This post is pure icing on the multilayered homemade cake that is homeschool. THIS IS A DECOR POST.

And yes, yes, I know there are many more important dimensions to homeschooling. But as I said, this is just icing. It’s just for fun!

When I realized I was going to have to educate my kids at home for at least another year, I wanted a dedicated space. Until then, we’d been mostly hanging out at the kitchen table. But since I had a room that was barely used, I figured… ehh, why not? I already had the desk and filing cabinet from CB2 and this Herman Miller Setu chair. The girls helped me pick the rug on RugsUSA. We wanted something that felt like a magic carpet because we’d just finished one of the Tales of the Alhambra. I splurged on the Grandin Road chair-and-a-half; we spend a lot of time reading in it.

A classic rhyme turned venn diagram. Chalkboard from Overstock.com

I shopped at different places in outfitting this school room. However, a favorite place to shop for homeschool stuff is thrift stores. I have found amazing, unique items for great prices.

First: BOOKS. I’ve found children’s classics, even hard-to-find ones, toddler books for my youngest, curricula in new condition, poetry anthologies, picture books. We use the local library a lot but it’s nice to have a home library, especially when you can get books for $.50-$1 or a paper bag’s worth at a library book sale for $5. I really think books are the most important thing to add to your home.

Picture book bookcase splurge from Land of Nod

Some 4th grade books! I got most of these on eBay. Bookcases: ikea.

You can find lots of wonderful things for your homeschool in thrift shops. Here are some ideas:

• Books (obviously!)
• Baskets of all sizes
• Kid furniture
• Dollhouses
• Games, toys, puzzles
• Seasonal/holiday decor
• Hatboxes and nesting boxes for storage
• Candles
• Office/desk supplies
• School supplies like bags of crayons, pencils, erasers etc.
• Abacus (handy for math and often found in the toy section)
• Globe
• Frames
• Vases, jars, containers
• Corkboards, white boards
• Wall hooks
• Art and handcrafted items
• Toy kitchens and play food
• Crafting items: yarn, stamps, paint sets

Globe, dollhouse, chair, sign: thrifted

My sweet mother in law thrifted this beautiful dollhouse for my girls. I found a wooden dollhouse furniture set for it on Amazon. The 16-inch Replogle globe was a major thrift find. Can you believe I paid $19 for this beauty? It just needed a little tightening at the base. The girls love looking at it. I got four of these art displays and the cursive board from Etsy.

Thrifted a couple beach chairs for backyard reading

Tea cups: Anthropologie. Tablecloth: Kate Spade. Antique poetry book: Biblio.com

Thrifted this bead maze

I find a lot of toys and puzzles at thrift stores. Since I’m often reading aloud, it’s important to have activities Sara can enjoy while we’re all together. Check out her production of Princess and the Frog! The frog is a Kiwico dissection toy (lol!) which she loves playing veterinarian with too. It was a Goodwill find. The play silks on the floor were thrifted too.

One of many baskets I’ve thrifted. This one holds library books.

Grandin Road chair-and-a-half is perfect for read-alouds

Isn’t this adorable?? I came across this sturdy, classroom-quality wood table and chairs that seemed perfect for our 4-year-old but I didn’t think I could fit them in my car. Well, the next morning my husband went and surprised me. I was so happy! The set was around $50 which is great considering these usually cost several hundred dollars at school-supply stores. The barn, soft counting book, expanding ball, and pencil holder were all thrifted too. I got the farm animals at the Lakeshore Learning store—highly recommend their toy sets for small hands. The wood pencil cup was just $1 and has an inscription on the bottom from a grandfather to a grandchild. Sometimes you find handmade things that were obviously made with a lot of care and I love the idea of extending their usefulness.

I think it’s fun to treasure hunt so I didn’t mind all the trips to little shops. Most of these items were compiled over the course of the last school year. My style is a mix of splurge and steal but after looking at thrift shops for a year, I’m confident I could find most stuff for a school room at thrift shops. The best advice I can give people new to thrifting: you have to go often and go with no plan. Sometimes I find nothing, sometimes just one thing. At busy thrift shops, you could go once a week and find an entirely new store. Get to know the extra discount days at your local thrift shops, e.g. two I go to regularly have 40%-50% off days. Scoop up any treasures and remember to be choosy. Don’t get anything that is just so-so or not priced well. Trust me: you will find something awesome eventually.